Gruppenanalyse mit elastischer Tensor-Normalisierung zur Generation von statistischen 3D-Atlanten der Nervenfaserstruktur
Die Diffusions-Tensor-Bildgebung (DTI) hat sich in den letzten Jahren zu einer leistungsfähigen Methode entwickelt, um den Verlauf der Nervenfasern in der weißen Hirnsubstanz in vivo darzustellen. Messgrundlage bildet die mikroskopische Diffusion von Wassermolekülen, die längs der Faserrichtung weniger eingeschränkt ist als quer dazu. Diffusions-Tensor-Bilder werden üblicherweise aufgenommen, indem Diffusionsgradienten in mindestens 6 linear unabhängigen Richtungen geschaltet werden, wodurch in jedem Voxel ein symmetrischer Tensor beschrieben wird. Die Hauptachse dieses Tensors stimmt mit der vermuteten Faserrichtung überein. Eine potentielle Anwendung dieser Technik ist die Untersuchung des Aufbaus und der Architektur der weißen Substanz innerhalb des Gehirns. In der konventionellen Kernspinbildgebung erscheint die weiße Substanz häufig nur als homogene Struktur, obwohl sie aus zahlreichen Axonbündeln unterschiedlicher Größe und Orientierung besteht. Durch die Verwendung der Richtungsinformation ist es möglich, verschiedene Axonengebiete in der homogen erscheinenden weißen Substanz zu unterscheiden. Diese spezielle Eigenschaft der Diffusionstensorbildgebung kann nützlich sein für Fragestellungen, bei denen die weiße Hirnsubstanz beurteilt wird bezüglich Entwicklung, Alterungsprozessen, Verlauf von Krankheiten und Regeneration nach Schlaganfall.
Die hier vorgestellte Software ermöglicht die gemeinsame Auswertung von Diffusions-Tensor-Daten von mehreren Personen womit die komplexe Architektur der weißen Substanz statistisch beschrieben werden kann und somit Unterschiede besser quantifiziert werden können. Verglichen mit der Registrierung von Volumina, die skalare Messgrößen enthalten, ist die räumliche Transformation von Tensor-Daten kompliziert, da sie zusätzlich Richtungsinformationen enthalten, die durch die Transformation beeinflusst werden. Diese Tatsache muss mathematisch mit berücksichtigt werden, um die anatomische Korrektheit der transformierten Volumina im stereotaktischen Koordinatensystem zu gewährleisten. Während eine starre Drehung des gesamten Volumens relativ einfach durchzuführen ist, ist die allgemeine elastische Transformation mathematisch anspruchsvoll. Die Software ermöglicht die vollständige Berücksichtigung der lokal affinen Transformationsparameter auf den Tensor. Durch die Normalisierung von Tensor-Daten zahlreicher gesunder Probanden kann ein probabilistischer Atlas aufgebaut werden, der als Grundlage für weitere Analysen dient. Durch die zu erwartende Reduzierung des Rauschens innerhalb der Atlasdaten wird die Verfolgung und Segmentierung der Faserbündel innerhalb der weißen Substanz zuverlässiger. Der Atlas stellt eine quantitative Größe zur Beschreibung der Verbindungsstärke zwischen einzelnen Regionen zur Verfügung und ermöglicht somit die statistische Erfassung von Unterschieden in der neuronalen Faserstruktur verschiedener Personengruppen.
Verfahren der elastischen Tensor-Normalisierung
Um die Effekte des Rauschens in einer Gruppenanalyse zu reduzieren werden die Daten von mehreren Personen mit Hilfe eines elastischen Registrierungsverfahrens in ein gemeinsames Koordinatensystem überführt. Die Normalisierung von Tensor-Daten erfordert eine Neuausrichtung des Tensors zusätzlich zur elastischen Verformung. Durch die Mittelung von normalisierten neuorientierten Tensor-Daten mehrerer Personen wird ein statistischer Atlas generiert.
Bei der elastischen Transformation der Messdaten in ein gemeinsames Koordinatensystem kommt es zur lokalen Verschiebung und Verformung der jeweiligen anatomischen Strukturen. Damit die Integrität der Strukturen insbesondere der Faserverlauf in der weißen Hirnsubstanz gewahrt bleibt, müssen die Tensor-Daten, die die Information über die Verlaufsrichtung der Fasern enthalten, entsprechend korrigiert werden. Abbildung 1 verdeutlicht dies.
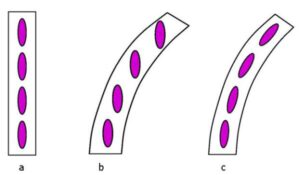
Abbildung 1: Die Tensoren müssen entsprechend der Verformung neu ausgerichtet werden. a) Ursrüngliches Tensor-Feld vor der Normalisierung. b) Verformtes Tensor-Feld ohne Neuausrichtung. c) Tensor-Feld nach der Transformation mit korrekter Neuausrichtung der Tensoren.
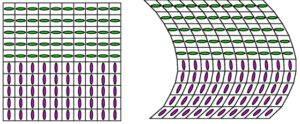
Abbildung 2: Da die Tensoren mikrostrukturelle Eigenschaften des jeweiligen Gewebes repräsentieren, müssen ihre Form und Größe erhalten bleiben, aber eine Neuausrichtung der Orientierung der Tensoren entsprechend der Verformung ist erforderlich. Mit der eigens entwickelten Software ist es möglich, sowohl die Effekte der lokalen Rotation als die Effekte einer Scherung vollständig zu berücksichtigen. Die erforderliche Neuorientierung hängt von der ursprünglichen Ausrichtung der Struktur ab. Eine separate Rotationsmatrix muss für jedes Volumenelement berechnet werden.
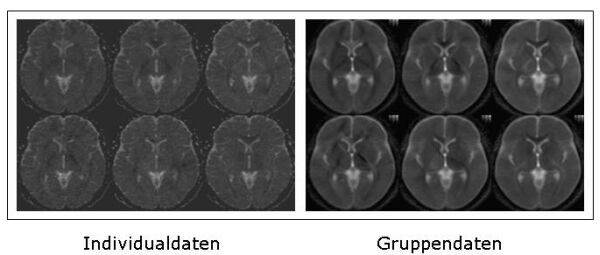
Abbildung 3: Durch die Mittelung der Daten mit korrekter Berücksichtigung der Richtungseigenschaften ist es möglich, den Rauschanteil zu vermindern und die Auflösung zu verbessern. Abbildung 3 zeigt einen Vergleich der Qualität der Diffusionsbilder zwischen Einzeldaten und Gruppendaten.
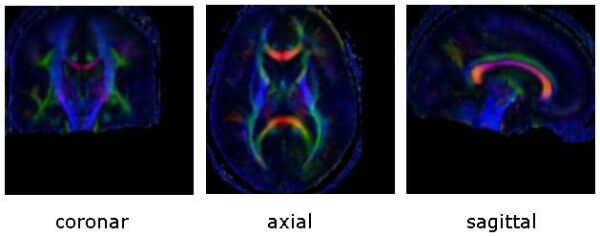
Abbildung 4: Darstellung von Individualdaten. Die Richtungsinformation der Hauptrichtung des Tensors kann mit sogenannten Richtungs-kodierten-Karten dargestellt werden. Hierbei werden Bildelemente, die Fasern enthalten, die von links nach rechts laufen in rot, Fasern von vorne nach hinten in grün und Fasern von oben nach unten in blau eingefärbt dargestellt. Die Bilder von Einzelprobanden zeigen auch Störungen durch messbedingtes Rauschen und geringe Auflösung.
Darstellung von Gruppendaten. Hingegen zeigen gruppengemittelte Bilder eine deutliche Verbesserung der Auflösung. Dies wird durch die Verwendung von Information aus mehreren Bildern ermöglicht. Daten in der ursprünglich geringen Auflösung werden an jeweils leicht verschiedenen Positionen aufgenommen. Durch Mittelung wird der Informationsgehalt erhöht, was eine verbesserte Auflösung ergibt. Verschiedene Faserbündel können klar unterschieden werden.
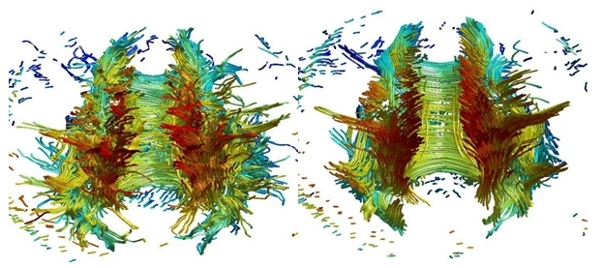
Abbildung 5: 3D-Rekonstruktion der Faserstrukturen
Die Software ist in der Lage die Richtungsinformation der Tensor-Daten zu nutzen, um mit einem speziellen Faserverfolgungsalgorithmus ein dreidimensionales Modell der Nervenfasern im Gehirn zu erstellen. Dieses Modell kann dann am Bildschirm aus jeder beliebigen Richtung betrachtet werden. Abbildung 6 zeigt Ergebnisse der 3D-Rekonstruktion der Faserverläufe jeweils für einen Datensatz einer Einzelperson bzw. einen normalisierten Gruppendatensatz. Der Verlauf der berechneten Bahnen im Individualgehirn erscheint gewunden. Der 3D-Faserverlauf der gemittelten Gruppendaten zeigt wesentlich stabilere Ergebnisse. Die Hauptnervenbahnen im Gehirn sind klar zu erkennen.