CADA – Continuous Autonomic Dynamics Analysis
Das hier beschriebene Verfahren stellt eine mathematisch-analytische Methode dar, mit der zeitvariable Schwingungssysteme in physiologischen Signalen beschrieben werden können. Sie basiert auf der Zerlegung eines realwertigen Signals 
in eine lokal stationäre, komplexwertige Repräsentation, deren Amplituden- und Phasenraum sich dynamisch entlang definierter Frequenzbahnen entfaltet. Dadurch wird die Herzratenvariabilität (HRV) nicht als statisches Spektrum, sondern als zeitkontinuierlicher Transformationsprozess der autonomen Oszillation beschrieben.
Neurowissenschaftlicher Kontext
Das autonome Nervensystem ist ein hierarchisch verschaltetes Rückkopplungssystem, dessen Aktivität durch fluktuierende Kopplung zwischen kortikalen, limbischen und medullären Strukturen geprägt ist. Die am ZNF zur Anwendung gebrachte Analytik erlaubt es, diese bidirektionalen Interaktionen in Form transienter Modulationen der Herzfrequenz zu erfassen, wobei sowohl sympathische Aktivierung als auch parasympathische Reaktivierung als phasenkohärente Oszillationsfelder modelliert werden.
Somit wird das autonome System als kontinuierlich deformierbares, nichtlineares Schwingungsnetzwerk beschrieben, dessen Frequenzcharakteristik sich topologisch in der Zeit verändert – eine Perspektive, die klassische spektrale Mittelwertbildungen nicht abbilden können.
Mathematische Grundlage
Formal lässt sich das CADA als Transformation einer reellen Zeitreihe in einen komplexwertigen, analytischen Signalraum 
auffassen, der durch eine frequenzspezifische Trägerfunktion definiert wird:
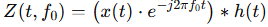
wobei 
eine glättende Integralkernfunktion beschreibt, deren Konvolutionsoperator selektiv jene Energieregionen extrahiert, die in der unmittelbaren Umgebung der Zielfrequenz 
liegen.
Der entstehende Komplexraum enthält eine zeitabhängige Amplitudenhülle
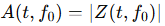
und eine lokal stationäre Phasenfunktion
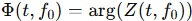
deren zeitliche Ableitung
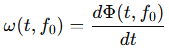
eine Momentanfrequenz ergibt, die das Oszillationsfeld als Funktion der Zeit aufspannt.
Die daraus resultierende Abbildung 
kann als nichtlineare Projektion eines hochdimensionalen Phasenraums interpretiert werden, in dem die spektrale Energie topologisch entlang kontinuierlicher Trajektorien verläuft. Durch diesen formal-analytischen Zugang wird die HRV zu einer Funktion zweiter Ordnung über dem Zeit-Frequenz-Raum — ein Konzept, das weit über das diskrete Leistungsdichtespektrum der Fourier-Analyse hinausgeht.
Grenzen klassischer Spektralverfahren
Die Fourier-Transformation (inkl. FFT) operiert unter der Annahme globaler Stationarität und linearer Superposition, womit alle Dynamiken auf einen globalen Frequenzraum abgebildet werden. Physiologische Prozesse hingegen sind inhärent nichtstationär, häufig sogar quasichaotisch, was bedeutet, dass die spektrale Energie zeitlich driftet und multiple Überlagerungen von Träger- und Modulationsfrequenzen entstehen. CADA löst diese Einschränkung, indem sie das Signal in einen gleitenden, frequenzparametrisierten Komplexraum überführt – eine Art lokaler analytischer Morphismus, der Momentancharakteristika anstelle globaler Mittelwerte beschreibt.
Algorithmische Umsetzung im ZNF
Die theoretische Grundlage der am ZNF realisierten Architektur beruht auf einer hybriden Signaltransformation im komplexen Hilbertraum, kombiniert mit nichtlinearen Regularisierungsoperatoren zur Stabilisierung der zeitlichen Amplitudenverteilung. Das Verfahren nutzt adaptive Integralkerne, deren Frequenzantwort sich dynamisch an das lokale Phasenfeld anpasst, sowie projektive Filtertransformationen, die Energie- und Phasenflüsse innerhalb definierter Subräume rekonstruieren.
Anstelle einer festen Parametrisierung erfolgt die Approximation der autonomen Schwingungen über rekursive Minimierung funktionaler Ableitungen im Raum der analytischen Signale. Dieser Ansatz erlaubt die simultane Schätzung von Amplituden, Phasen und Frequenzdrift als gekoppelte Differentialprozesse – eine Modellierung, die die klassische lineare Filterlogik der FFT vollständig hinter sich lässt.
So entsteht ein hochauflösendes, kontinuierliches Abbild der autonomen Aktivität, das auf der Interaktion mehrerer dynamischer Operatoren basiert, deren Stabilität durch spektral gewichtete Regularisierung und phasenadaptive Glättung gewährleistet wird.
Anwendung: Parasympathische und sympathische Reaktivierung
In Untersuchungen zur kardio-vagalen Erholung nach körperlicher Belastung zeigte sich, dass diese Analysemethode im Gegensatz zur herkömmlichen Herzfrequenzerholung ein frühes, hochsensitives Abbild der parasympathischen Reaktivierung liefert. Bereits 40 s nach Belastungsende trennen sich die Amplitudenverläufe signifikant zwischen trainierten und untrainierten Probanden. Trainierte Personen zeigen eine überproportionale, transient-hyperbolische Zunahme der HF-Aktivität, während bei untrainierten die Reaktivierung verzögert und abgeschwächt verläuft.
Gleichzeitig werden sympathische Rückstellprozesse (LF-Band) als gegenphasige Dynamiken sichtbar, was eine quantitative Analyse des sympathovagalen Gleichgewichts in Echtzeit erlaubt.
Wissenschaftliche und klinische Bedeutung
Die beschriebene zeitkontinuierliche Modellierung autonom-nervöser Oszillationen transformiert die HRV-Analyse von einer deskriptiven zu einer prozess-analytischen Methodik. Sie erfasst die zeitlich gekoppelten Regulationsmechanismen des autonomen Nervensystems und bildet damit eine Grundlage für die funktionelle Diagnostik vegetativer Dysbalancen, die Prävention stressbedingter Erkrankungen und die Erforschung zentral-autonomer Interaktionen.
Damit wird die HRV nicht länger als statischer Index interpretiert, sondern als dynamisches, neuronales Regulationsmuster, das die Funktionsfähigkeit zentraler und peripherer Steuerungssysteme im Takt des Lebens selbst beschreibt.